On the Sparsity of L1 Regularization
Let’s define some important terminology / concepts.
$L_p$ Norms
An $L_p$ norm is a way to calculate the magnitude of a given mathematical object, say a vector, $\vec{x}$ in $\mathbb{R}^2$.
\[\vec{x} = \begin{bmatrix}2 \\ 2\end{bmatrix}\]If I measure its magnitude via the $L_2$ norm, commonly known as the euclidean distance, I get:
\[\sqrt{2^2 + 2^2} = \sqrt{8} = \text{Norm}_2(\vec{x})\]while for the $L_1$ norm, i’d get a simple $3$.
More generally, the $L_p$ norm is defined as:
\[\text{Norm}_p(\vec{x}) = \sqrt[p]{|x_1|^p + ... + |x_n|^p}\]Scalar Fields
They’re quite simple, despite their name making the underlying concept sound more intimidating than it needs to be.
Given a function, $f$, $f$ represents a mathematical function that takes an input in an $n$-dimensional space, $\mathbb{R}^n$, and outputs a value $\in \mathbb{R}$, a simple scalar.
\[f: \mathbb{R}^n \rightarrow \mathbb{R}\]As an example, a type of scalar field is the $L_p$ norm, as:
\[f: \mathbb{R}^n \rightarrow \mathbb{R}, \hspace{3mm} \text{Norm}_p(\vec{x}) = \sqrt[p]{|x_1|^p + ... + |x_n|^p}\]where $\text{Norm}_p(\vec{x})$ represents the scalar output of the $L_p$ norm.
Isosurfaces and Isolines
Isolines are curves on a graph, where an arbitrary scalar field $f$, takes on a constant value, $c$, which is called a level set.
As an example, for a function $f(x, y) \in \mathbb{R}^2$, the isolines can be defined as the set of points, $(x, y)$ where:
\[f(x, y) = c\]You can also think of them as contour lines. For the $L_p$ norm, the contour lines are symmetric!
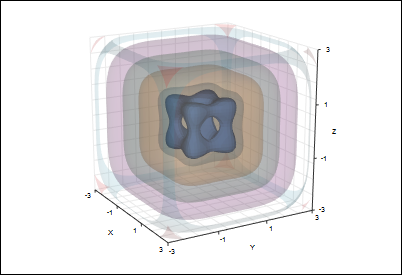
For spaces $\mathbb{R}^n$ where $n = 3$, the isolines turn into isosurfaces, where we have a $3$ dimensional shape.
 </img>
$w = x^4 . + y^4 + z^4 - (x^2 + y^2 + z^2 - .4), \hspace{2mm}\text{ Level Set: 0 for Blue}$
</img>
$w = x^4 . + y^4 + z^4 - (x^2 + y^2 + z^2 - .4), \hspace{2mm}\text{ Level Set: 0 for Blue}$
For $n > 3$, we have isohypes, though visualizing their shape becomes pretty difficult.
Sparsity of $L_1$, in Gradient Descent
Let’s take a look on how we define $L_1$ regularization for a neural net, onto our minimization function.
\[\hat{\phi} = \text{argmin}_{\phi}[\mathcal{L}(\phi, Y) + \lambda ||\phi||_1]\]| where $\mathcal{L}$ is our loss and $\lambda | \phi | _1$ represents the penalty term, equivalent to the magnitude, in the $L_1$ metric space, of our parameters $\phi$, multiplied by the regularization hyperparameter $\lambda$. |
If $\mathcal{L}(\phi, Y)$ is $0$, the minimum value of the loss is the $L_1$ norm (or level set) of $\phi$ multiplied by $\lambda$. The set of parameters, $\phi$ can only be minimized to the degree that they yield a minimum of the loss while still meeting the minimum $L_1$ norm.
Via gradient descent, our neural network could try to minimize the value of the $L_1$ norm, but doing so moves the set of $\phi$ into the opposite direction of the minima of the loss.
 </img>
<em style = > Countour lines are the loss, the edges of the diamond are the isolines of the $L_1$</em>
</img>
<em style = > Countour lines are the loss, the edges of the diamond are the isolines of the $L_1$</em>
As you notice, the minima of the $L_1$ could be simply reduced to $0$ at the origin. But of course, we’re also trying to find the minima of the loss, at the center of the black contour lines.
Therefore for this problem, our best minima lies on the axis, at the intersection of the contour line of the $L_1$ and the outermost contour line of the loss, at one of the axis…
…where one of the values of our set of parameters, $\phi$, is $0$.
More generally, regularization via the $L_1$ norm promotes sparsity as the $\text{argmin}_{\phi}$ of $L_1$ regularized loss lies on the direction of a a single axis of the $\mathbb{R}^n$ space given by $\phi$.
This lies on the corners of the diamond, formed by the isolines of the $L_1$.
 </img>
</img>
Purely considering $\mathbb{R}^2$, the nearest point to the true minima of the loss on the isolines of the $L_1$ is typically $\in (c, 0), (0, c), (-c, 0), (0, c)$ where $c$ is the level set for $\phi$.
Then typically, given a $\phi \in \mathbb{R}^2$,
\[\text{argmin}_{\phi} \in (c, 0), (0, c), (-c, 0), (0, -c)\]| where $c$ is the level set of $ | \phi | _1$. Your parameters become sparse! |
Note, typically!
The construction of your loss function, $\mathcal{L}$, may not always promote sparsity!
It’s important to take a look at your loss function, when you want sparse $\phi$’s!
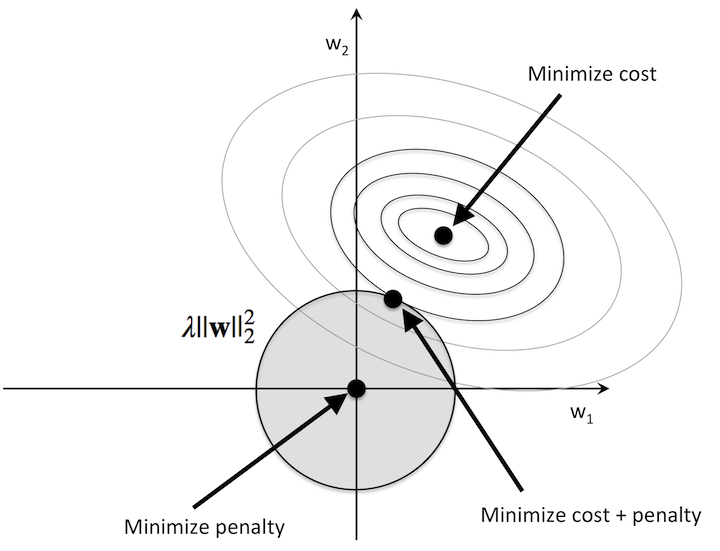
In the case of $L_2$ regularization, sparsity tends to not be the case. The isolines of the $L_2$ norm don’t yield a diamond but instead compose a circle around the origin.
 </img>
</img>
Then, the minima of the $L_2$ regularized loss doesn’t lie on the axis, but instead at an arbitrary point within the subspace of the $L_2$ metric space of $\phi$.
Choose your regularizer carefully!